In trying to learn about ALS Matrix Factorization I realized there wasn’t any easy intuitive explanation. So I made this one!

The theory

R:{uxi}

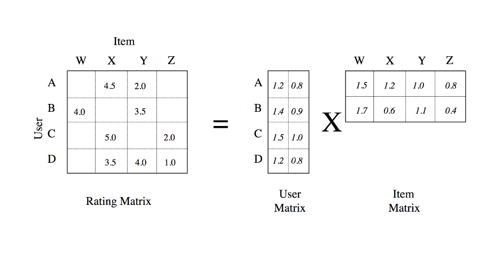
R is our rating matrix. Every row is a user, and every column is an item. Each cell then corresponds to a user rating an item. We will represent a single rating as the lower case value r, and any specific r that corresponds to a user u and an item i is written as rui. What may be interesting to note is that there are missing values within our rating matrix, we’ll put zeros in there for now.

X:{kxu}, Y:{kxi}

These two matrices are called factors, where when we multiply the user matrix X by the item matrix Y we get the original size of our rating matrix R. To find a specific user’s rating of an item rui we then take a submatrix calculation:

\[r_{ui} = x_{u}y_{i}^{T}\]

The only problem is that these two smaller matrices X,Y that are multiplied together don’t get a good estimation of the original matrix R as we simply put random variables in them to start off with.

Alt text

An optimization problem needs three things:

  • Values to correct
  • A prediction
  • A ground truth

    • And we have:

  • Our factor matrices X,Y
  • The resulting prediction R
  • The observed R


    • Let’s use least squares as a loss function! Then the following will be our equation:

    \[\min_{X,Y} \sum\limits_{observed\ r_{ui}} (r_{ui} - x_{u}^{T}y_{i})^2\]

    Another issue is that we need a regularizer such that we don’t overfit!

    \[\min_{X,Y} \sum\limits_{observed\ r_{ui}} (r_{ui} - x_{u}^{T}y_{i})^2 + \lambda(\sum_{u}\lVert x_{u}\lVert^2+\sum_{i}\lVert y_{i}\lVert^2)\]

    Should we use gradient descent? Well, no. It’s slow and this problem is nonconvex. Instead we’ll use alternating least squares (ALS), where we fix one variable as a constant and minimize for the other, then visa versa. Remember, xu is a 1xk vector in the X matrix.

    — Algorithm —

    Initialize X, Y

    for k slice of X
    \(x_{u} = (\sum_{r_{ui}\in r_{u*}} y_{i}y_{i}^T+\lambda I_{k})^{-1}\sum_{r_{ui}\in r_{u*}}r_{ui}y{i}\)
    end for

    Now do the same for loop for Y. That’s it! Do this until we converge, or stop gaining accuracy in our training set.

    So what does the code look like?

    There’s a full repository here. The only difference in the implementation is that A and B are substitute matrices that represent the following:

    \[x_{u} = (A + \lambda I_{k})^{-1}*B\]

    where

    \[A = y_{i}y_{i}^{T}\]

    and

    \[B = rating*y_{i}\]

    for every rating item in u.

    The code shown below is how the ALS matrix factorization code is actually implemented.

    def als_step(train_matrix, x, y, variable, k, lmbda):
    """
    ALS Step as defined by x = (sum(y*yT) + reg)^-1 * sum(rating*y)
    or y = (sum(x*xT) + reg)^-1 * sum(rating*x)
    :param train_matrix: True matrix with validation scores taken out.
    :param x: x factor
    :param y: y factor
    :param variable: If either x or y is being updated
    :param k: Factor length
    :return: Updated factor chosen by variable
    """
    regularization_matrix = np.multiply(lmbda, np.identity(k))
    num_users, num_items = train_matrix.shape

    if variable == "x":
        for u_index in range(num_users):
            # A and B block calculations
            r_u = train_matrix[u_index, :]
            r_ui_indices = np.nonzero(r_u)
            A = np.zeros((k, k))
            B = np.zeros((k, 1))

            # Looking at every Rui
            for r_ui_index in r_ui_indices:
                y_i = y[r_ui_index, :].reshape((k, 1))
                A += np.dot(y_i, y_i.T)
                B += r_u[r_ui_index] * y_i

            try:
                x[u_index, :] = np.dot(np.linalg.inv(np.add(A, regularization_matrix)), B).reshape(k)
            except np.linalg.LinAlgError:
                # Occurs when the determinant is zero. Use try-except to handle such cases.
                pass
        return x
    elif variable == "y":
        for i_index in range(num_items):
            r_i = train_matrix[:, i_index]
            r_ui_indices = np.nonzero(r_i)
            A = np.zeros((k, k))
            B = np.zeros((k, 1))

            for r_ui_index in r_ui_indices:
                x_i = x[r_ui_index, :].reshape((k, 1))
                A += np.dot(x_i, x_i.T)
                B += r_i[r_ui_index] * x_i

            try:
                y[i_index, :] = np.dot(np.linalg.inv(np.add(A, regularization_matrix)), B).reshape(k)
            except np.linalg.LinAlgError:
                # Occurs when the determinant is zero. Use try-except to handle such cases.
                pass
        return y

    So to use more mathy terms after explaining this simply. We’ve created a latent space through the custom rank k that we’ve embedded all of the users and items into.

    Thank you for reading! Hopefully this was helpful, and at some point if it’s worth investigating, I’ll include Probabilistic Matrix Factorization on this blog too. 🙂